Topological Insulators
A Cookie Jar Analogy
A topological insulator can be compared to a metal cookie jar filled with insulating cookies. The electric current can only flow outside through the metal box. In the case of a topological insulator, however, the metal and the cookies are made of the same material.

The Quantum Riddle
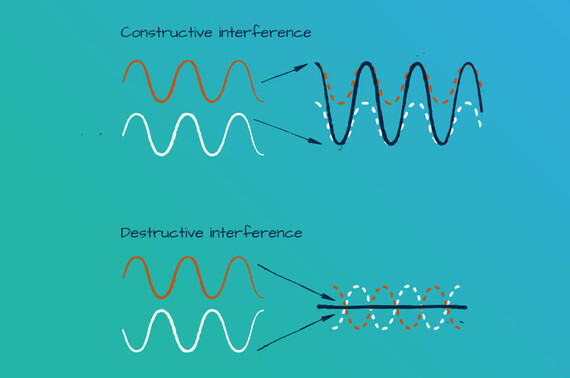
Sometimes waves, sometimes particles? The mysterious world of quanta does not differentiate so strictly. Electrons, the basis of modern chip technology, are quantum objects with wave properties. If waves overlap, they can amplify or cancel each other out - a phenomenon known as constructive or destructive interference.
Conduct or Insulate?
Metals like copper or gold are good electrical conductors, glass or ceramics are instead electrically insulating. These properties are linked to the wave nature of the electrons in a material. Microelectronics is based on the ability to switch materials specifically from an electrically conductive to an insulating state - or vice-versa. In semiconductors, the negatively charged electron waves are scattered by the electric fields of the atomic nuclei of the crystal lattice and can overlap, i.e. interfere with each other. By applying a voltage, one can control whether this superposition is constructive (electrically conductive) or destructive (insulating). With this, the basis for computer chips is created. However, the electron waves can be controlled much more precisely.
Spectakular! The Quantum Hall Effect
Extreme precision: In 1980, the physicist Klaus von Klitzing, at that time a private lecturer at the Physics Institute in Würzburg, discovered the quantum Hall effect. This opened the door to a new field of solid-state physics – and he received the Nobel Prize in Physics in 1985.
This is how this spectacular effect comes about: the electrons in a transistor are subjected to an external super-strong magnetic field, 500,000 times stronger than the Earth's magnetic field. Outcome: Inside, the transistor becomes an insulator, while electron waves with perfect conductivity surround its edge. The Hall conductivity is even more extraordinary: it is quantized and is exactly an integer multiple of e2/h (e = elementary charge, h = Planck constant) – accurate to 15 digits! This sensational precision of the new quantum effect is based on the principles of topology, a branch of mathematics.

Topological Insulator: It Works!
The quantum Hall effect is controlled by a super-strong magnetic field - which is unsuitable for day-to-day practical applications. That's why a long search was conducted for similar effects that work without a magnetic field. The breakthrough came 25 years later: The electrical conductivity of mercury telluride (HgTe) was investigated at the Chair of Experimental Physics 3 at the University of Würzburg. This investigation revealed properties that could not be explained with conventional models. A worldwide research boom began when Professor Laurens W. Molenkamp and his team succeeded in 2007 in providing the world's first experimental proof of a topological insulator.
Quantum Physics meets Einstein
In addition to the electric charge, electrons also have a magnetic moment, called spin. The spin is influenced by magnetic fields and surprisingly plays a role even when no external magnetic field is applied! According to Einstein's theory of relativity, the spin perceives the electric fields in a crystal as effective magnetic fields when the electrons move through the crystal lattice. By skillfully tailoring the material’s composition and crystal lattice, this phenomenon can be used to induce insulating behavior inside and perfectly conductive edges – just like the quantum Hall effect. A strong external magnetic field is therefore unnecessary because the electrons bring their own.
Charles L. Kane and Eugene J. Mele first proposed this concept of the topological insulator in 2005 for graphene, a honeycomb lattice of carbon atoms. However, graphene proved to be unsuitable for the experimental proof of topological behavior. For light waves, however, this geometry works very well.
Resistance-Free
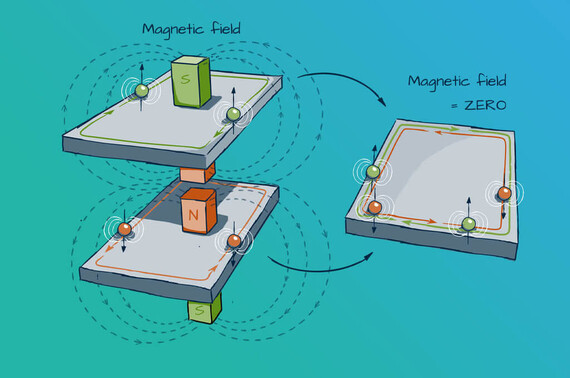
The Quantum Spin Hall Effect is comparable to two copies of the Quantum Hall Effect for magnetic fields of opposite directions. When the two states are added, the magnetic fields compensate each other. This results in two boundary conduction states running in opposite directions with opposite spin orientation. The effect of the latter is that both channels allow an unhindered flow of current in opposite directions without resistance or loss. This occurs solely due to the internal structure of the material, independent of the details of the edge. After all, in topology an edge is always an edge, no matter how crooked or frayed it is.
Calculating with Spins
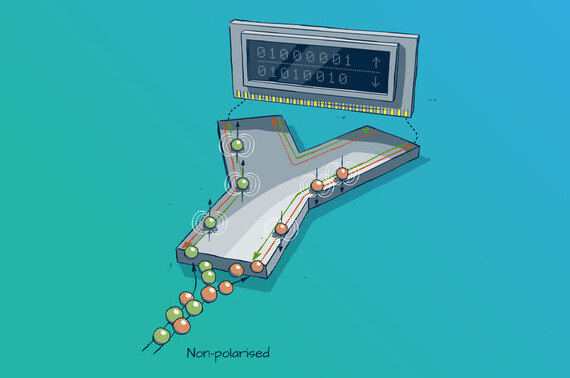
By means of the Quantum Spin Hall Effect (QSHE), new types of electronic components that calculate with electron spins are possible without the use of external magnetic fields. The figure shows that the QSHE can be used to separate electrons according to their spin.
This arrangement is suitable both for the generation of spin-polarized currents and for their analysis, since only spins of one type can flow along one channel (red or green). Without the use of external magnetic fields, information can be magnetically encoded, transported and thus used for spin transistors – which is what spintronics is all about.