Introduction

Prospects of quantum information technologies have motivated an intense search for systems, which intertwine topology and electronic correlations1,2,3,4. Strongly interacting and spin–orbit-coupled electrons on the honeycomb lattice, as theoretically described by the Kane–Mele–Hubbard model5, feature quantum spin Hall (QSH), Mott–Hubbard, collective magnetic and chiral superconducting states. While several weakly interacting QSH systems are now well-studied experimentally2,6, material realizations of honeycomb Kane–Mele–Hubbard fermions with strong correlations and spin–orbit coupling are rare7,8. Here, we introduce a new “van der Waals engineering” platform to serve this purpose.

We show that stacking of 1T-TaSe2 into bilayers can deconfine electrons from a deep Mott insulating state realized in the monolayer to a system of correlated Dirac fermions subject to sizable spin–orbit coupling. Central to this transition is the possibility of van der Waals materials to stack in different configurations. For a specific honeycomb arrangement (Fig. 1) the kinetic energy associated with the electronic hopping t turns out to be of the same order of magnitude as the effective local Coulomb repulsion U. The system features, therefore, electronic correlations, which turn out to put the system right on the verge between QSH and correlated antiferromagnetic insulating states at charge neutrality and support chiral superconductivity under doping. We finally demonstrate that tuning the system via electric fields and twisting of the layers relative to each other sensitively affects the low-energy electronic structure in terms of emerging Dirac mass and spin–orbit coupling terms and leads to completely unexplored regimes of correlated electrons.

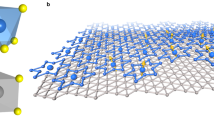
Fig. 1: Crystal structures of 1T-TaSe2 mono- and bilayers in the CCDW phase.
figure 1

a Monolayer 1T-TaSe2 in the CCDW phase. Only Ta atoms are shown. The Ta atoms are distorted into a SoD pattern, where the central Ta atoms (red) are surrounded by two rings of in total twelve Ta atoms (black). The SoDs are marked with red lines as guide to the eyes. b Top and three-dimensional side view of honeycomb-stacked CCDW 1T-TaSe2 bilayer. Only the Ta atoms in the SoD centers are shown, with blue spheres and shaded regions marking the bottom layer atoms, and red spheres and shaded regions for the top layer. The inset illustrates the leading terms of the effective low-energy Hamiltonian, i.e., the nearest-neighbor hopping t = −34 meV and the local interaction U ≈ 130 meV. c Side view of 1T-TaSe2 bilayers embedded in field effect transistor structures for the application of vertical electric fields. A non-twisted and a 180∘ twisted bilayer are shown with Ta atoms (red and blue) and Se atoms (yellow).

Full size image

Results and discussion

From a correlated insulator to emergent Dirac fermions

Layered group-V transition metal dichalcogenides (TMDCs) such as 1T-TaSe2 or 1T-TaS2 feature a low-temperature commensurate charge density wave (CCDW) where Ta-atoms are displaced into Star-of-David (SoD) patterns (Fig. 1a)9,10. In this phase, the SoDs form a triangular \(\sqrt{13}\times \sqrt{13}\) superlattice in every layer and host correlated electrons: 1T-TaS2 shows a metal-to-insulator transition when entering the CCDW phase10. In 1T-TaSe2, the bulk remains conductive till lowest temperatures, while the surface exhibits a Mott transition around 250 K11,12. Recently, 1T-TaSe2 has been fabricated down to monolayer thickness13,14,15 and a pronounced thickness dependence of the electronic structure has been reported15. As bonds between the layers are mainly of van der Waals type, different stacking configurations are observed in experiments16,17 and have a strong impact on the electronic structure18,19,20.

We compare the CCDW state in the monolayer to a bilayer with honeycomb stacking, where the SoD centers form a buckled honeycomb lattice (Fig. 1b). The bottom layer SoD centers form sublattice A and the top layer sublattice B. This stacking is one of many possible configurations, which can generally differ, both, by the local atomic stacking and by the stacking of the SoD centers. The local stacking considered here, has the Ta atoms of the bottom layer approximately beneath the lower Se atoms of the top layer (Fig. 1c). While this kind of local stacking is not the most commonly observed one of the T-phase TMDCs15,17, a corresponding stacking sequence has been found in transmission electron microscopy studies of 1T-TaS217 and turns out to be metastable in density functional theory (DFT) simulations of 1T-TaSe221. Regarding the stacking of the SoD centers further van der Waals DFT total energy calculations (see Supplementary Information) show that the particular honeycomb arrangement studied here, is metastable and energetically on the order of 10 meV per formula unit above the lowest energy configuration. This is similar to the configuration observed experimentally in ref. 15 and it is thus plausible that also the honeycomb configuration considered here, is within reach of experiments. Experimental approaches including tear-and-stack22 and Scanning Tunneling Microscopy voltage pulse-based manipulation schemes23 can present possible avenues to control and switch metastable stacking configurations and to reach the honeycomb configurations discussed in our paper. At small twist angles all different kinds of configurations can be realized locally in the moiré, including likely those honeycomb cases discussed here.

To study the electronic structure of such engineered stackings, we combine ab-initio calculations in the frameworks of DFT and the random phase approximation (RPA) with effective low-energy models, which we investigate with dynamical mean-field theory (DMFT) and two-particle self-consistent (TPSC) many-body approaches, see “Methods” section.

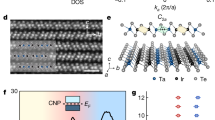
In the CCDW phase, the band structure of monolayer 1T-TaSe2 obtained with non-spin-polarized DFT is characterized by a single (Ta) flat band at the Fermi level10,18,19,20, which has a bandwidth of less than 20 meV (Fig. 2a, left). Hence, the CCDW formation largely quenches in-plane hopping of the electrons. In the honeycomb-stacked bilayer (with no twist), two dispersive bands with a bandwidth of the order of 200 meV emerge from the low-energy flat band of the monolayer (Fig. 2a, right). Comparison of the mono- and bilayer bandwidths shows that interlayer hopping effects must dominate over intralayer hoppings by approximately an order of magnitude. In this sense, CCDW TaSe2 bilayers are the exact opposite of graphene bilayer systems, since in the latter out-of-plane coupling is an order of magnitude weaker than in-plane hopping24,25. For the 1T-TaSe2 honeycomb bilayer, the upper and lower low-energy bands touch as Dirac points at the Brillouin zone corners K and K'. In the undoped system, these Dirac points are exactly at the Fermi level.

Fig. 2: Electronic structure and phase diagram of CCDW 1T-TaSe2 systems.
figure 2

a Band structures of CCDW 1T-TaSe2 monolayer (left) in comparison to honeycomb-stacked non-twisted CCDW 1T-TaSe2 bilayer (right). Bottom panels show a zoom around the Fermi level EF. The red and dashed blue lines mark the DFT low-energy bands without and with SOC included, respectively. From the flat band near EF in the monolayer (red solid line, bandwidth ≈ 14 meV) two dispersive bands with a bandwidth ≈ 200 meV emerge in the bilayer case. The bilayer bands exhibit Dirac points in the Brillouin zone corners, K and K'. b Influence of extrinsic Semenoff mass terms ΔM on the low-energy band structure. The sublattice character is color coded. The system changes from QSH to trivial band insulator at ΔM = 0.82 meV, which corresponds to a vertical electric field of Ez ≈ 0.5 mV Å−1. c Quasi-particle weight Z for non-twisted CCDW 1T-TaSe2 bilayer calculated with DMFT and TPSC. Both approaches place the system consistently in the moderately correlated regime Z ≈ 0.75 at all calculated temperatures. d Temperature-dependent antiferromagnetic correlation length ξAFM and inverse static spin susceptibilities of non-twisted CCDW 1T-TaSe2 bilayer at wave vector q = 0 as calculated with TPSC. The intra-sublattice (1/χAA = 1/χBB) and inter-sublattice (1/χAB) elements of the inverse susceptibility at wave number q = 0 are shown. e Schematic phase diagram of honeycomb-stacked non-twisted CCDW 1T-TaSe2 bilayer as a function of extrinsic Semenoff mass ΔM and interaction strength U. The region accessible for non-twisted CCDW 1T-TaSe2 bilayer through tuning with external electric fields is highlighted. The transition from QSH to band insulator is a continuous transition at small U (dashed line) and a first-order transition at larger U (solid line). The red area in the quantum spin Hall region indicates the increasing many-body character of this phase.

Full size image

We next construct a Wannier Hamiltonian to describe the Dirac bands with one Wannier function for each SoD center, i.e., two Wannier orbitals per bilayer CCDW superlattice unit cell (Supplemental Fig. 2). The resulting nearest-neighbor hopping between a sublattice A site in the bottom and a neighboring sublattice B site in the top layer amounts to t = −34 meV and is the leading term of the Wannier Hamiltonian. There are further terms in the Wannier Hamiltonian, which are, however, at least an order of magnitude smaller than t.

The effective Hubbard interaction U for the SoD Wannier orbitals of CCDW TaSe2 calculated in RPA is U ≈ 130 meV, which is also in line with the experimental estimates in ref. 15 and calculations for TaS219. The ratio of hopping to Coulomb interaction is decisive in determining the strength and kind of electronic correlation phenomena taking place. Our calculations yield U/∣t∣ ≈ 3.8.

To study the resulting electronic correlations, we performed simulations of the Hubbard model for the non-twisted CCDW 1T-TaSe2 bilayer in the framework of DMFT and the TPSC approach26,27. The quasi-particle weight Z shown in Fig. 2c is a measure of the electronic correlation strength. In the temperature range T = 60–230 K, both DMFT and TPSC consistently yield essentially constant Z ≈ 0.75. Our system is thus at intermediate local correlation strength and far away from the paramagnetic Mott–Hubbard transition taking place above UMott/t ≈ 8.2. The DMFT and TPSC studies of the full Hubbard model for the non-twisted CCDW 1T-TaSe2 bilayer are, thus, in line with studies of the idealized Hubbard model on the honeycomb lattice28.

The TPSC calculations give insight to spin-fluctuations taking place in the system (Supplemental Fig. 4). The inverse intra- and inter-sublattice terms of the static magnetic susceptibility at wave number q = 0, as well as the antiferromagnetic correlation length ξAFM are shown in Fig. 2d. We observe that antiferromagnetic fluctuations with alternating spin orientation between the two sublattices (A, B) are dominant and strongly enhanced at temperatures T ≲ 100 K. These fluctuations indicate that the non-twisted CCDW 1T-TaSe2 bilayer is close to a quantum phase transition from a Dirac semimetal to an antiferromagnetic insulator, which occurs for ideal Hubbard honeycomb systems exactly in the range of Uc/t ≈ 3.6–3.86,29,30.

Spin–orbit coupling

The aforementioned magnetic correlation phenomena are sensitive to details of the low-energy electronic structure and spin–orbit coupling (SOC), which we discuss in the following based on a symmetry analysis. The space group of non-twisted CCDW 1T-TaSe2 bilayer in the honeycomb structure is \(P\bar{3}\) (#147), comprising inversion symmetry and three-fold rotations C3 around an axis perpendicular to the bilayer. Imposing also time-reversal symmetry, every band must be two-fold degenerate. Therefore, SOC-induced qualitative changes of the band structures can occur near the Dirac points at K and K′. A corresponding k ⋅ p expansion (see Supplementary Information) reads

$$\begin{array}{ll}{H}_{{\rm{0}}}=\hslash {v}_{{\rm{F}}}(\tau {k}_{{\rm{x}}}{S}_{{\rm{x}}}+{k}_{{\rm{y}}}{S}_{{\rm{y}}})+{\lambda }_{{\rm{SOC}}}\tau {\sigma }_{{\rm{z}}}{S}_{{\rm{z}}}\\ +{\alpha }_{{\rm{R2}}}({k}_{{\rm{x}}}{\sigma }_{{\rm{y}}}-{k}_{{\rm{y}}}{\sigma }_{{\rm{x}}}){S}_{{\rm{z}}},\end{array}$$
(1)

where the pseudospin S describes the sublattice degree of freedom, σ acts on the electron spin, and τ = ±1 labels the valley (K, K′) degree of freedom. This Hamiltonian comprises three contributions; the first contribution is a two-dimensional massless Dirac term, with the sublattice-pseudospin playing the role of the spin inherent to the Dirac equation. This term is analogous to the massless Dirac term in graphene6,24,25. SOC is responsible for the second and third contributions to H0: a valley–spin–sublattice coupling λSOC = 0.74 meV, which is often called Kane–Mele spin-orbit term31,32, and a sublattice-staggered Rashba term αR2, which belongs to the R2 class according to the classification form ref. 33. A finite Kane–Mele term λSOC opens a gap and turns the system described by H0 into a QSH insulator31,32. Importantly, the Kane–Mele term here is enhanced in comparison to its counterpart in graphene by two orders of magnitude24,25,34, and corresponds to a temperature T ≈ 10 K, which is well accessible in experiments. Given that U/∣t∣ ≈ 3.8, the non-twisted CCDW 1T-TaSe2 bilayer implements a material realization of the Kane–Mele–Hubbard model in a regime very close to the topological quantum phase transition from a QSH insulator to an antiferromagnetic insulator (Fig. 2e).

Dirac fermions and their topology are affected by different kinds of mass fields. An energy difference between electrons localized in sublattice A and B leads to a so-called Semenoff mass term M, which would enter the Hamiltonian H0 of equation (1) in the form MSz. This term breaks sublattice invariance and thereby inversion symmetry and leads to a transition from a QSH to a band insulator at ∣M∣ = ∣λSOC∣31,35. In the non-twisted CCDW 1T-TaSe2 bilayer, the intrinsic Semenoff mass M0 = 0 is required to vanish by symmetry. Our Wannier construction yields M0 = 0.14 meV, which is small as compared to all other relevant terms in the system. Possible origins of this small symmetry breaking can be the Wannier constructions and also faint asymmetries accumulated during self-consistency iterations in the DFT calculations. Vertical electric fields Ez, as realizable in field effect transistor geometries (Fig. 1c), break inversion symmetry, translate into staggered sublattice potentials, and therefore corresponding extrinsic Semenoff mass contributions ΔM (Fig. 2b). DFT calculations (Supplementary Fig. 3) yield the approximate relation ΔM ≈ eEzd/ϵ⊥, where d = 6.4 Å is the interlayer distance, e is the elementary charge, and ϵ⊥ = 3.72 plays the role of an effective dielectric constant. The QSH to band insulator transition is reached for Ez ≈ 0.5 mV Å−1 = 50 kV cm−1 (Fig. 2b), which is well within reach of experiments36.

Taken together, our calculations show that the honeycomb-stacked non-twisted CCDW 1T-TaSe2 bilayer is located in a region of the phase diagram (Fig. 2e) with three different phases (QSH insulator, band insulator and antiferromagnetic insulator) coming together. Electron correlation is known to change the order of the QSH-band insulator transition from second to first-order37. Contrary to the standard non-interacting QSH to band insulator transition, where the gap closes and reopens continuously with vanishing gap at the transition point, the QSH gap remains finite and the system changes discontinuously to a band insulating state at the transition point. Application of vertical electric fields in the system at hand represents hence a possibility to realize this exotic interaction-induced first-order transition.

Twisted CCDW 1T-TaSe2 bilayers

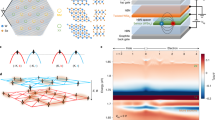
Layered van der Waals systems allow to realize different stacking configurations via twisting, i.e., relative rotations between the layers. General twist angles θ lead to incommensurate moiré patterns superimposed to the CCDW lattice. Arguably the simplest case of twisting is a rotation angle of θ = 180∘, which leads to a system with identical Bravais lattice but different symmetry of the supercell basis (Fig. 1c): in case of honeycomb stacking of the CCDW, the space group of the 180∘ twisted structure of CCDW TaSe2 bilayer is reduced to P3, meaning that inversion symmetry is lost with respect to the non-twisted case. The resulting band structure (Fig. 3a) is qualitatively similar to the non-twisted honeycomb case regarding the overall shape and width of the low-energy bands. Thus, also the 180∘ twisted case will be far away from the paramagnetic Mott transition. However, the low-energy band structure is markedly different in the 180∘ twisted case. First, the conduction band is almost flat between K and M. Second, inversion symmetry breaking lifts band degeneracies: our DFT calculations reveal a staggered potential and an associated intrinsic Semenoff mass term of M0 = 8.55 meV, which opens a gap at the K and K' points already without SOC and without external electric fields. Furthermore, additional SOC terms are now allowed by symmetry (see Supplementary Information) and completely lift the remaining band degeneracies except for the time-reversal symmetric points Γ and M.

Fig. 3: Influence of 180∘ twisting and electric fields on band structure and topology.
figure 3

a Band structure for 180∘ twisted CCDW 1T-TaSe2 bilayer without (solid red) and with (dashed blue) SOC included. The degeneracy of the bands is lifted due to the absence of the inversion symmetry after twisting. b Influence of vertical electric fields on the low-energy band structure for 180∘ twisted CCDW 1T-TaSe2 bilayer. The gap at K closes and a band touching point occurs when the Semenoff mass term is ∣M∣ = ∣M0 + ΔM∣ = 1.87 meV at Ez = –4.2 mV Å−1. c Non-interacting λR vs. ΔM topological phase diagrams for non-twisted, 180∘ twisted CCDW bilayer and two cases in between, where the spin–valley coupling B of the non-twisted CCDW 1T-TaSe2 bilayer is varied. For B = 0 the system shows the symmetric onion-like shape similar to ref. 31. When B increases, the QSH region shrinks and disappears when B = λSOC. For B > λSOC, the system behaves as a trivial band insulator. The yellow arrows in the leftmost and rightmost panels indicate the path in phase space accessible by varying the vertical electric field Ez.

Full size image

Based on a symmetry analysis, we obtain the following low-energy model in the vicinity of K and K′:

$$\begin{array}{ll}{H}_{18{0}^{\circ }}\,=\,{H}_{{\rm{0}}}+{M}_{{\rm{0}}}{S}_{{\rm{z}}}+B\tau {\sigma }_{{\rm{z}}}\\ \qquad\qquad+\,{\lambda }_{{\rm{R}}}(\tau {\sigma }_{{\rm{y}}}{S}_{{\rm{x}}}-{\sigma }_{{\rm{x}}}{S}_{{\rm{y}}})+{\alpha }_{{\rm{R}}1}({k}_{{\rm{x}}}{\sigma }_{{\rm{y}}}-{k}_{{\rm{y}}}{\sigma }_{{\rm{x}}})\\ \qquad\qquad+\,{\lambda }_{{\rm{D}}}(\tau {S}_{{\rm{y}}}{k}_{{\rm{x}}}-{S}_{{\rm{x}}}{k}_{{\rm{y}}}){\sigma }_{{\rm{z}}}.\end{array}$$
(2)

The additional terms with respect to the non-twisted honeycomb structure equation (1) are the intrinsic Semenoff mass (M0), the spin–valley coupling term (B), the Kane–Mele–Rashba interaction (λR), and a Rashba interaction belonging to the R1 class33 giving rise to pure Rashba spin-polarization patterns (αR1). The last term (with coupling constant λD) can also be seen as an effective k-dependent magnetic field parallel to the z-axis. Our DFT calculations yield M0 = 8.55 meV, B = −1.85 meV, ∣λSOC∣ ≲ 0.05 meV and λR = 3.21 meV. These terms affect the dispersion and imprint an intricate sublattice and spin structure to the low-energy bands, which can be manipulated by vertical electric fields as shown in Fig. 3b.

Except for Ez = −4.2 meV Å−1 (ΔM = −6.68 meV and M = M0 + ΔM = 1.87 meV), the system is always gapped. We calculated the Z2 topological invariant for the non-interacting 180∘ twisted bilayer in comparison to the non-twisted bilayer case,, as well as for two cases in between where the ratio B/λSOC is varied (Fig. 3c, and Supplemental Information). In the non-twisted bilayer, the system is in a QSH state unless an extrinsic sufficiently large Semenoff mass term or an additional Rashba SOC term λR are added. In the 180∘ twisted case, the situation is very different regardless whether or not the intrinsic Semenoff mass term is compensated by an external electric field and regardless of λSOC. Indeed, many changes in the SOC terms suppress the QSH state in the 180∘ twisted bilayer: The comparably large Rashba λR and the spin–valley coupling terms B and a strong reduction in λSOC. Each of these alone is sufficient to suppress the QSH state. At vertical electric field Ez = −4.2 mV Å−1 the gaps at K and K' close, and a band touching point emerges.

While it is clear that there will be tendencies towards interaction-induced (quasi)ordered phases as well, here, the kind of ordering is likely different from the non-twisted case but largely unexplored. The band touching at Ez = −4.2 mV Å−1 implements a situation similar to saddle points in a two-dimensional dispersion, where already arbitrarily weak interactions would trigger different kinds of magnetic or excitonic instabilities38. How these instabilities translate into the intermediately correlated and strongly spin–orbit-coupled case of 180∘ twisted TaSe2 is a completely open question.

Conclusions and outlook

The field of twistronics with materials like bilayer graphene is based on the idea that weak interlayer coupling can flatten highly dispersive bands and thereby boost electronic correlations39,40,41. The system introduced here takes the opposite route of deconfining formerly Mott localized electrons. This approach should be generally applicable to interfaces of Mott localized electrons under two conditions: the interlayer coupling should substantially exceed the in-plane one and at the same time define a connected graph linking all sites of the system. Possible example systems range from stacking faults in the bulk of CCDW layered Mott materials17 to molecular systems42.

Especially the twisting degree of freedom opens new directions to experiments. Since interlayer hopping is the dominant kinetic term in deconfined Mott systems like bilayers of CCDW 1T-TaSe2, we expect incommensurability effects to be much more pronounced than in twisted graphene systems39. θ = 30∘ twisted CCDW 1T-TaSe2 bilayer should realize a quasicrystal with twelvefold rotation symmetry and provide an experimental route to correlated electrons and emerging collective states in a quasicrystalline environment.

The prototypical case of CCDW 1T-TaSe2 bilayer demonstrates how deconfinement of Mott electrons leads to exotic states of quantum matter: the non-twisted bilayer approaches a quantum tricritical region of competing QSH, trivial band insulating, and antiferromagnetic insulating states. At 180∘ twist angle different kinds of electrically controllable band degeneracies with associated many-body instabilities, hypothetically of excitonic type, emerge. Clearly, the phase space for manipulating deconfined Mott electrons is high dimensional. We here identified the combination of twist angle and perpendicular electric field as decisive for TaSe2 bilayers. Further means to control emerging electronic states include dielectric engineering43 and charge doping. Our calculations showed that the non-twisted CCDW 1T-TaSe2 bilayer in honeycomb stacking approximates the (Kane–Mele) Hubbard model on the honeycomb lattice with U/∣t∣ ≈ 3.8 very well. In this regime, doping the system away from the Dirac point towards the van Hove singularity is expected to lead to chiral superconductivity44,45,46,47, most likely of d + id-type.

Methods

DFT calculations

We perform DFT48,49 calculations by using the Vienna ab-initio simulation package (VASP)50,51 with the generalized gradient approximation of Perdew, Burke, and Ernzerhof (GGA-PBE) for the exchange-correlation functional52,53. We obtain the total energies, relaxed structures and electronic structure of mono- and bilayer 1T-TaSe2 systems. We calculate the total energies for various possible stackings in undistorted and CCDW bilayer 1T-TaSe2 using Γ-centered k-meshes of 15 × 15 × 1 and 9 × 9 × 1, respectively, and taking into account van der Waals (vdW) corrections within DFT-D2 and cross-checking with DFT-D354,55, see Supplemental Fig. 1. The ionic relaxation is done using the conjugate gradient algorithm until all force components are smaller than 0.02 eV Å−1.

Since the DFT-D2 corrections yield correct interlayer distances but do not correctly capture the CCDW distortions, we adopted the following relaxation procedure to calculate the commensurate \(\sqrt{13}\times \sqrt{13}\) CCDW bilayer structures:

  1. 1.

    We perform relaxations for a \(\sqrt{13}\times \sqrt{13}\) supercell of the monolayer (without vdW corrections), using a superlattice constant of a = 12.63 Å according to ref. 15. We fix the vertical positions of the Ta atoms, while allowing for Ta in-plane displacements. The Se atoms are allowed to freely relax in all three directions.

  2. 2.

    We include then a second layer and optimize the interlayer distance, d, while keeping all relative intralayer distances fixed. We find d = 6.4 Å for the ideal honeycomb stacking in CCDW bilayer 1T-TaSe2.

  3. 3.

    We relax the CCDW bilayer following the same procedure described for the monolayer, i.e., without vdW corrections and vertical positions of the Ta atoms according to the optimized interlayer distance d fixed, while allowing for in-plane displacements. The Se atoms are allowed to freely relax in all three directions.

We cross check the results obtained by this procedure against calculations with vdW corrections according to the DFT-D3 method55. In contrast to DFT-D2, the CCDW distortions are well described in the DFT-D3. Thus, full relaxations of all atomic positions have been performed in the DFT-D3 framework for the mono- and bilayer. Both our step-by-step procedure using DFT-D2 method, and the full relaxation using DFT-D3 give equivalent results for the total energies (see Supplemental Fig. 1b), for the crystal and band structures.

For the non-collinear magnetic calculation, i.e., when SOC is included, we set the net magnetic moment to zero in all atoms of the unit cell, and use a Γ-centered k-mesh of 6 × 6 × 1.

Estimation of the screened Hubbard interaction U via RPA

We estimate the local Hubbard interaction U for the flat bands around the Fermi level in the CCDW 1T-TaSe2 bilayer from the ab-initio calculation of the screened Coulomb interaction, using RPA for the undistorted bilayer. We follow a similar procedure as in ref. 56, which we summarize below:

  • We initially calculate the WANNIER90 tight-binding model for the three low-energy Ta bands \({\mathcal{C}}\), whose orbital character is mostly \(\{{d}_{{z}^{2}},{d}_{{x}^{2}-{y}^{2}},{d}_{xy}\}\) (see Fig. 2(a) in ref. 56) in the undistorted monolayer 1T-TaSe2.

  • The static RPA-screened Coulomb interaction tensor Wαβγδ(q, ω → 0) is calculated for undistorted monolayer 1T-TaSe2, where q is a reciprocal wave vector on a Γ-centered mesh of 18 × 18 × 1, and \(\alpha ,\beta ,\gamma ,\delta \in {\mathcal{C}}\). We neglect q = 0 terms in our RPA analysis in order to avoid unphysical effects.

  • In the CCDW 1T-TaSe2 bilayer, the \({d}_{{z}^{2}}\) orbitals from Ta atoms in the SoD centers have the largest contribution for the bands around the Fermi level. Thus, for each q, we consider only the tensor element W(q) ≡ Wαααα(q) with \(\alpha ={d}_{{z}^{2}}\).

  • Then, the local Hubbard interaction U in a single star of David is calculated by averaging over the \({d}_{{z}^{2}}\) orbital weight from each Ta atom (labeled by \({w}_{{d}_{{z}^{2}}}({\bf{R}})\)) in the star of David:

    $$U=\mathop {\sum}\limits_{{\bf{R}},{\bf{R}}^{\prime} \in {\davidsstar} }{w}_{{d}_{{z}^{2}}}({\bf{R}})U({\bf{R}}-{\bf{R}}^{\prime} ){w}_{{d}_{{z}^{2}}}({\bf{R}}^{\prime} )$$
    (3)

    where U(R) is the discrete Fourier transform of W(q).

DMFT and TPSC many-body calculations

For non-twisted CCDW 1T-TaSe2 bilayer, we construct tight-binding-Hubbard Hamiltonians of the type

$${H}_{{\rm{TBH}}}=\mathop {\sum}\limits_{\langle i,j\rangle ,\sigma ,{\sigma }^{\prime}}{t}_{ij}^{\sigma {\sigma }^{\prime}}{c}_{i\sigma }^{\dagger }{c}_{j{\sigma }^{\prime}}+U\mathop {\sum}\limits_{i}{n}_{i\uparrow }{n}_{i\downarrow }$$
(4)

from a Wannierization of the ab-initio DFT band structure (Supplementary Information), and estimate the on-site repulsion U to be about 130 meV by means of RPA calculations. We study these effective low-energy models from a many-body perspective to judge the type of correlations in the system. In DMFT the lattice Hamiltonian is mapped onto a self-consistently determined single impurity problem, solved—in our case—within numerical exact quantum Monte Carlo in the hybridization expansion flavor (CT-HYB) (for a review, see57). The resulting sublattice-resolved self-energy, Σ, is local (k-independent) but it contains frequency-dependent non-perturbative corrections beyond Hartree-Fock to all orders and can account for Mott–Hubbard metal-to-insulator transitions. All DMFT calculations are performed using w2dynamics58. The double counting is accounted for using the fully localized limit. For two-dimensional systems it is important to estimate non-local effects at the level of the self-energy, not included in DMFT. To this goal, we apply the TPSC method59, which produces accurate results in the weak-to-intermediate coupling regime, if compared to lattice quantum Monte Carlo calculations in the single band Hubbard model. For non-twisted CCDW 1T-TaSe2 bilayer, which is modeled by a multi-band system we use the multi-site formulation of TPSC26 while neglecting the Hartree term to avoid double counting of correlation effects already accounted for in DFT. Moreover, to be able to apply TPSC to this system we project out spin off-diagonal terms and take only the diagonal spin-up contributions from DFT while still assuming a paramagnetic state. The combination of TPSC accounting for the k-dependence of Σ and DMFT, in which we can include all off-diagonal terms between spin-orbitals and access antiferromagnetic ordering at strong coupling consitutes a powerful tool to determine the many-body nature of 1T-TaSe2.